Hello, and welcome to a great wonderful article series on competitive programming and DSA. We are preparing for technical interviews, and coding contests to ace product-based companies. Taking our preparation forward over bit manipulation where in the last article we have studied some popular bit hacks and how we can use bitwise operators to speed up some heavy operations. In this article, we will solve most asked coding problems under bit manipulation so let's get started with high josh.
Table of Contents
- Find the lone set bit coding question
- find value whose XOR with a given number of maximum.
- find number of mismatching bits in 2 number
- Find non-repeating numbers in an array
- Application-based problems on bit manipulation
- Swap two numbers without a temporary variable
- Find power set of array
- Find duplicate elements in an array
- Toggle K number of bits
- Set K number of bits
- Reset all bits in a binary representation of the number
- End Notes
1) Find the lone set bit
The problem statement is interesting. Given a non-negative integer whose binary representation contains only one set bit (one occurrence of 1) and all the remaining bits are 0. Your task is to find the position of 1 in the binary representation of numbers. And if a number has more than one occurrence of 1 in binary representation then print -1.
🔰NOTE - The position of the set bit must be counted from the least significant bit (LSB).
Example
The first line contains the number of test cases. Each test case contains only a single integer. You have to print a position of 1 if the binary representation has only one occurrence of 1. Else print -1.
Approach to find the position of 1 in a binary representation of a number
In our previous blog, we studied that the number which has only one occurrence of 1 are the numbers which are a power of 2 like 4(100), 8(1000), 16 (10000), etc. So what we can do is we can check each number as is it a power of 2 that means only one set bit is there so we can convert it in binary form. And reverse the binary representation and find the occurrence of 1. Or without reversing using modulus also we can find a position of 1. if a number is not the power of 2 then simply print -1.
💻Code ~ I hope that you can implement the code now because we have already done with the code of checking the number is the power of 2 or not. And after that, you only have to write an If-Else statement.
def isPowerOf2(num):
return not(num & (num-1))
def findBinary(num):
return bin(num).replace("0b", "")
def findSetBit(N):
#if the num is 0 then return -1
if N == 0:
return -1
#check num is power of 2
elif isPowerOf2(N):
#power of 2 then find binary and pos of 1
bin_n = findBinary(N)
bin_n = bin_n[::-1]
res = bin_n.index("1")
return res+1
#simply return -1
else:
return -1
print(findSetBit(4))
2) Find a value whose XOR with a given number is maximum
Given an integer X, your task is to find an integer Y such that bitwise XOR of the integers X and Y give the maximum possible value with 64 bits. The integer Y should not be greater than 2305843009213693951 ((2^61)-1).
🔰 Note
- The maximum obtainable value of XOR can be stored in 64 bits memory space.
- The given number X is non-negative.
Example
The first line contains several test cases. Each test case contains only a single integer X. Print the maximum possible value of Y such that XOR of X and Y give maximum value in 64 bits.
💡 Approach to find maximum value for maximum results XOR
Think a little bit that XOR operations give 1 when both the bits are different and result in 0 when both the bits are the same. Hence, to ensure the maximum value of XOR, we need to set all the ON which are OFF in binary representation of X. So for that Y can have 1 where bits of X are 0 and Y can have 0 where bits of X is 1. Thus, Y is nothing but 1s complement of X.
💻 Code - We can easily find the Y using the left-shift operator. The number of bits to kept answers less than is 61.
def XORWithGivenNumberIsMaximum(X):
num_bits = 61
#find Y which is 1s complement of x in 61 bit
res = ((1 << num_bits)-1) ^ X
return res
3) Find Number of mismatching bits
Given two non-negative numbers. your task is to find the number of bits that do not match in a binary representation of both the numbers.
Example
The first line contains the number of test cases. each test case has space-separated numbers in a single line. you have to print several mismatched bits in both numbers.
🔖 How would you approach the problem?
The naive approach that everyone will think of is to find the binary representation of both the number and use brute force to compare each bit and increase the count. Some who will think a little bit ahead of it is maximum there is 32 number of bits in the binary representation of a number so simply iterate 32 times and using left shift operator compare Ith bit of each number. The code of this approach is shown below.
def numberOfMismatchingBits(first, second):
ans = 0 #store no. of mismatched bits
# loop till 32 to check ith bit is same of not
for i in range(32):
if (first & (1 << i)) != (second & (1 << i)):
ans += 1
return ans
print(numberOfMismatchingBits(4, 5)) 💡 XOR-based approach for finding mismatched bits in two number
The above approach will work fine but will result in TLE in some large test cases so to optimize the approach we can use XOR. Now we know that when 2 bits are the same then XOR gives 0 and only results 1 when bits are different. So we can perform an XOR operation between two numbers and the number which we get in the result will hold several set bits that are different in two numbers so simply find the number of set bits present in resultant XOR.
def numberOfMismatchingBits(first, second):
xor = first ^ second #find xor of both num
ans = 0
#number of set bits in xor
while xor > 0:
xor = xor & (xor - 1)
ans += 1
return ans
print(numberOfMismatchingBits(4, 5))
4) Find Non-Repeating Numbers
Given an array of size N in which all the elements occur twice except two number that appears only one time. Your task is to find the two non-repeating numbers.
Example
The first line contains T denoting the number of test cases. Each test case has N denote the size of the array followed by array elements in the next line. you have to print two space-separated numbers.
How would you approach the problem to find non-repeating numbers in an array?
Most of the people will follow the hashmap (frequency map) approach in that we will iterate in an array and find the element whose occurrence is one in an array and print the results.
def findNonRepeating(arr):
# Return a list of 2 integers
res = []
arr_set = set(arr)
for i in arr_set:
if arr.count(i) == 1:
res.append(i)
return res
💡 XOR Operation Approach
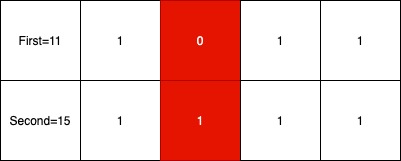
We can use the bitwise XOR operation to solve this problem. we know that XOR of two same numbers results in zero. Suppose we have an array as [36, 50, 24, 56, 36, 24, 42, 50]. Now if we find XOR of all the arrays then the resultant XOR will be 56 ^ 42. This is not the XOR of 56^42 but also the XOR of all arrays. The resultant number will be 18 (010010). Now how we can use this resultant XOR to separate two non-repeating numbers. So think of a little bit and observe each bit. The binary of resultant XOR will contain a set bit where both the bits of two non-repeating numbers will be different. This is a very important point to be noted so using this we can separate two sets such that find the rightmost set bit of XOR. Observe the 2nd bit of each array element so the elements which have 2nd bit as set bit are [50, 24, 50] and the elements that have a second bit as zero are [36, 24, 56, 36, 24] so when you perform XOR of this two sets separately you will be left out with two non-repeating number in an array.
Read the approach twice and observe the below figure for more clearance and solve it on paper.
So, let us discuss step by step algorithmic approach.
- First, find the XOR of all the numbers in an array so the resultant XOR will contain A^B of two elements that occur only one time.
- Find the rightmost set bit. In other words, perform bitwise and with its 2's complement.
- initialize two variables say X and Y that will store two non-repeating numbers.
- traverse gave array and check that if bitwise and of set bit and array element is greater than 0 then store bitwise XOR of array element and X. Else store bitwise XOR of array element and Y.
- The resultant two numbers will store the two non-repeating numbers.
def findNonRepeating(arr):
# Initialize a variable to store XOR of all numbers.
temp = arr[0]
# Finding XOR of all numbers.
for i in range(1,len(arr)):
temp = temp ^ arr[i]
# Initialize a variable to store rightmost set bit of temp.
setBit = (temp & ~(temp-1))
# Initialize variables to store non-repeating numbers.
x = 0
y = 0
for i in range(len(arr)):
if((arr[i] & setBit) > 0):
x = x ^ arr[i]
else:
y = y ^ arr[i]
#two number are non-repeating
return x, y
NOTE - Now the questions which we will solve are application-based questions that you can solve using different approaches but with the help of bit manipulation tricks and bitwise operators complexity can be minimized. So, the only request is to solve and understand the below questions with full interest and concentration because questions will seem very easy to you but the approach you will follow will have large complexity.
5) Swap Number without using a temporary number
The question is very simple and it is not required to explain a problem statement because you have solved this question many times. These questions ins mostly asked in interviews of service-based companies. Given two numbers and your task is to swap both numbers such that both variables hold alternate values.
Example
Arithmetic operator-based approach to swap two numbers
Most people will use arithmetic operators and mostly will use addition and subtraction to swap two numbers. First, add both numbers and then to get the second number to subtract second from first and same again to get the first number.
def swapNumber(x, y):
x = x+y
y = x-y
x = x-y
return [x, y]
Multiplication and Division Operators - some people do follow the multiplication approach to swap two numbers like first multiply both numbers and to get one divide the multiplication with the corresponding number.
def swapNumber(x, y):
x = x * y
y = x // y
x = x // y
return [x, y]
print(swapNumber(10, 5))
Twist in question - Now the interviewer asks you to swap two numbers without using a temporary variable as well as suggest to not use arithmetic operators. now, how will you swap two numbers with an arithmetic operator and without a temporary variable.
💡 Bitwise XOR Approach to swap two numbers
Now comes the XOR operator in play when you can use XOR property X^0 = X and X^X = 0. with these properties swap the numbers X and Y.
- X = X^Y
- Y = X^Y. It is the same as (X^Y) ^ Y so the result will be X.
- X = X^Y. It is the same as (X^Y) ^ X so the result will be Y
💻Code - try to implement the code.
def swapNumber(x, y):
# Edge case when given two variable are same.
if(x == y):
return [x, y]
x = (x & y) + (x | y)
y = x + (~y) + 1
x = x + (~y) + 1
return [x, y]
6) Power Set
Given a sorted array of N number of integers. Your task is to generate the power set of the array where each subset of the power set is sorted. Power set is defined as an array of all possible subsets of an array.
🔰 Note - For every subset X present in the power set must be sorted. The order of subset in the power set does not matter, only they need to be sorted.
Example
First-line contains the size of the array followed by space-separated array elements in the next line.
💡 Bit manipulation Approach to find all subsets of a set
The question is the same as generating all the subsets of the array. most of the people will use the brute-force approach, and those who have followed our recursion tutorial will try to build this using recursion because we have solved this question using recursion. But time complexity increases using recursion too in this. We know that an array of length N has 2^N subsets. So the approach is simple to run a loop til 2^N-1 and check whether the binary representation of I has been set off or not. If the bit is set to a bit in the binary representation of I then add that position element in the current subset till N-1 and the subset in the final subset list. I hope that the approach is clear to you and can build the algorithm easily.
💻 Code - In our case array is sorted so we do not need to add the current subset in sorted order but if an array is unsorted then you have to sort the current subset before adding it in the resultant set.
#code
def powerSet(arr):
allsubsets = []
n = len(arr)
for i in range(2**n):
curr_subset = []
for j in range(n):
#if jth bit is set bit in binary of i
if (i & (1 << j)):
curr_subset.append(arr[j])
allsubsets.append(curr_subset)
return allsubsets
arr = [1,2,3]
ans = powerSet(arr)
print(ans)
7) Find Duplicate Element in Array
Given an array of size N containing each number between 1 to N-1 at least once. Only one integer in an array is present twice. Your task is to find the duplicate element present in an array.
Example
The first line contains T denoting the number of a test case. Each test case has two lines in which the first line contains N (size of an array), and the second line contains array elements.
💡 Bitwise XOR Approach to find a duplicate element in an array
We have used XOR in almost all questions and I hope that you can think of an approach to solve this question. suppose we have an array [1, 2, 3, 4, 4] of size 5 where it contains elements between 1 to N-1. let us understand the approach using this example step by step way.
- find the XOR of an array where the element that will present twice will become zero and result in 1^2^3.
- Now we will again perform its XOR from 1 to N-1. So, the element which was canceled out will only remain in the result as (1^2^3) again undergo XOR with (1^2^3^4).
- Hence we are left with duplicate elements because now it is present at odd times and the rest all are present even a number of times.
💻 Code - We can implement the code easily with a few lines of code.
def findDuplicate(arr):
n = len(arr)
arr_xor = arr[0]
#find the xor with arr element and position
for i in range(1, n):
arr_xor = arr_xor ^ arr[i]
arr_xor = arr_xor ^ i
return arr_xor
8) Toggle K number of bits
Given a 32-bit integer N and an integer K. Your task is to toggle the K number of bits in a given integer and return the new integer.
Example
The first line contains T denoting the number of test cases. Each test case contains space-separated integers as N and K.
How you would approach the problem?
Most beginners will think of this basic approach. First, convert the number into binary form and check that if the length of binary representation is greater than K then toggle K number of bits from the right. Else first add K - length(binary) number of zeros to binary representation and toggle each bit of binary form. now if we do so the code will be very long and the time complexity is O(K). And think on the approach so we can do this directly using the left shift operator in a loop of k times. The approach is known as iteration with bit manipulation.
def toggleKBits(n, k):
# This function returns updated number
# after toggling the given K bits.
for i in range(k):
n = n ^ (1 << i)
return n 💡 Bit Manipulation approach
The above approach may lead to TLE so we can solve it in O(1) time. The idea is simple to extract the rightmost K bits and toggle them. Then after clearing the rightmost K bits from the original integer, store the toggle bits back to the original number.
- To extract rightmost K bits use lastbits = (N & ((1 << k)-1))
- to clear the rightmost K bits we can perform complement of it like N = (N & ~((1 << k)-1)).
- Toggle the extract last K bits
- Add the toggle last bits to the original number. N = N + last bits
This can be done in constant time, and space complexity. Now try to implement the approach using python. The code snippet is given below.
9) Set K Bits
Given a number N. your task is to set the bits from 0 to kth position. In simple words, you have to make att the bits of number as a set bit between 0 to k and return the new number. For example, given number is 5 and k is 2. binary of 5 is 101 and after setting two bits the binary form becomes 111, and the result will be 7.
Example
Given an N and K for different test cases. you only need to implement the function and return the resultant answer.
How would you approach the problem (Brute-force method)
The basic approach every one of us will think of is to iterate k times and for each bit between it take its OR with 1 (set bit) so the bit will become set bit and return the resultant number.
def setKBits(n, k):
# Iterating and manually set k bits of the number.
for i in range(k):
# Temp holds the value of integer whose only ith bit is set.
temp = (1 << i)
# Update the number by performing Bitwise OR.
n |= temp
return n 💡 Bit Manipulation Approach
The approach costs O(K) and for some large test cases, it may reach TLE. The basic idea is to make a set bit only 1 bit. what we were doing in the brute-force method was setting every bit till less than k. so it is similar to setting a kth bit and subtracting that by 1. (for example, 7 (0111) = 8((1000)-1). here k is equal to 3. store this is temporary variable and just perform bitwise OR of number N with temporary variable and return the results.
💻 Code - let us build the algorithm.
def setKBits(n, k):
#Temp will store the value where only the kth bit is set in number.
temp = (1 << k)
#Decrement the temp by 1 to make every bit set that are smaller than K.
temp -= 1
# Update the number by performing Bitwise OR.
n |= temp
return n
10) Reset All bits
The question is very similar to the above one. Given an integer N(32 bits). your task is to make all the bits zero that are right os the most significant bit (MSB). suppose the given integer is 45 (101101). Then after making all the bits zero after MSB the binary form becomes 100000.
Example
Given T number of test cases and each test case contains a single line integer N.
💡 Approach to Reset all the bits of a number
The problem is very simple which basically ask you to find the greatest number that is smaller than the given number and is a power of 2 because after making all the bits as 0 except MSB then it will be a power of 2 because every number that has only one set bit is the power of 2. So the approach is simply that first find the position of MSB. to find a position of MSB you can use a loop till the number is greater than 0 and update the number by dividing by 2 and increasing the count. Now simply find a power of 2 MSB times and return the answer.
💻 Code - implement the algorithm and try it on your own.
def resetAllExceptMSB(n):
if n == 0:
return 0
msb = 0
n = int(n/2)
#find position of MSB
while n > 0:
n = n//2
msb += 1
return (1 << msb) # 2**msb
End Notes
Congratulations! If you have followed this tutorial till the end then I must say that you have really enjoyed each and every coding problem we have discussed and the approach of bt manipulation and got to learn how bitwise operators help to optimize the code in a simple and easy way within one or two lines of code.
👉I hope that it was easy to catch each and every problem with ease. If you have any queries, then feel free to post them in the comment section below or you can reach out to us through this contact form.
Thank you! 😊