Hello and welcome to the wonderful article series on competitive programming. We have already completed our first topic of study and practiced a lot of questions in Recursion. If you have followed and gone through previous parts Or you are familiar with recursion then most welcome and you can continue to Backtracking. Otherwise, I would like to request you to first visit our Recursion blog and get an idea of how to build a recursive approach and How it works so you will get a clear idea of how to think of a solution for a particular problem and the topic we are about to start is very closely related to Recursion or you can say as an advance version of Recursion. So now, I hope that you are familiar with Recursion and good to go with Backtracking.
Table of Contents
Brief Overview on Backtracking
Backtracking is an approach where we recursively try to find all possible ways to reach a destination from an initial point and at any point, if we find we cannot move forward then we ignore that way and backtrack from there and come back and explore the different way. This is only the approach of Backtracking. Let's take an example like your friend says I have kept one bag at end of one street from your home that goes towards the temple, and he asks you to find the bag. Now there are different streets from your home to reach the temple so you will start from street number one, and you did not find anything then you will come back, and explore the second street, there you find some hurdle to go so you again come back, then explore the third street and in the same way till you reach and finds the bag you explore each street means you are backtracking from the current path to explore new possibility So, all this happens in Backtracking.
What Kind of Problems comes under Backtracking?
This is the question asked by most beginners like How will I identify like I need to use Recursion of Backtracking. So this will automatically come to your mind with a little bit of consistent practice. But I want to tell you in backtracking some specific types of problems lies which are discussed below.
1) Decision Making ~ It means the problem where you have choices like whether to go left, down, up, or down. These types of problems mostly reside under backtracking.
2) Permutations ~ To find all possible permutations of any sequence data type we can use backtracking.
3) Subsets ~ Programming question where we are supposed to find all possible subset, subsequence-like things from any sequence data type then they are mostly solved using Backtracking.
How to Identify the Backtracking Problem
Some basic points that help in identifying the problem are backtracking.
- Exponential Complexity or Factorial Complexity ~ You will be given that solution can be expected in exponential complexity because you have to explore each and every path.
- Constraints ~ If complexity is more then obviously constraints will be less like N is less than 500.
- No guarantee that which path to go first to find a solution because you are asked to find any solution or all possible solutions.
The concept of Backtracking will more clear when we will solve some questions on it. So let's get to our first question.
1) Subsets of a Set
It is one of the amazing problems under Backtracking, and let's pick this as our first problem in Backtracking. So the problem statement is given a set of distinct integers. So problem statement is simple where we can form a different subset of one single set. So let us first understand the backtracking approach and then we will see how to code it and what points to remember.
Example
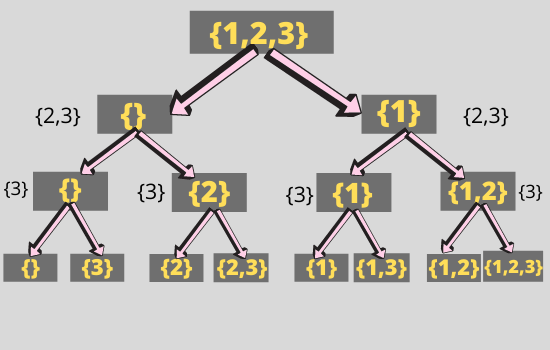
Explanation - One we can have an empty set as a subset of set and break all integers with every other element which forms a subset. on reversing a subset it is also a subset because both are the same so keep only one.
💡 Backtracking Approach to find subsets of a set
Now the main idea is how should we approach it. So first think of a recursive approach and try to build a recursive binary tree. So if we start from the initial array so in subset we have two choices. The first is to ignore taking any element means to let it be empty and another is added one element to subset from an array. And recursively perform this operation in the length of the array and after adding one element in an array and performing recursion we have to bring subset to initial position because next time again we have to take subset as empty so this operation is called backtracking. Observe the below recursive tree to get more clearance about the approach.
💻 Code - Let us implement the approach using Backtracking in python. 👇
def findAllSubset(arr, subset, idx):
print(*subset)
for i in range(idx, len(arr)):
subset.append(arr[i])
#Recursive call for each forward element
#so set with 1 element as well as double and further will be in res
findAllSubset(arr, subset, i+1)
#remove the arr[i] from subset for doing backTracking
subset.pop(-1)
return
arr = [1,2,3]
subset = []
idx = 0
findAllSubset(arr, subset, idx)
2) Generate All Valid IP Addresses
One more interesting problem in backtracking. The problem statement is something like we are given a string containing only digits. our task is to generate all possible IPv4 Address combinations and print each combination in lexicographic order.
🔰NOTE - A valid IPv4 address contains exactly four integers. each integer is between 0 and 255 separated by single dots, and cannot have leading zeros except in the case of zero itself. read the example snippet below to get a better idea about what the IPv4 address should look like.
Input and Output Format
Now have a look at sample Inputs and sample output. The first line of each input contains several test cases and from the second line, each line of a test case contains a string of digits. For each test case print all possible IPv4 addresses.
Approach to Solve the Problem 😃
Each four-part of IP address should be in the range of 0 to 255. To generate all possible approaches we need to break a string into four different parts and check whether each part is a valid part or not. If it is valid then we will form its combination by placing the dots and saving the solution. So we can approach this problem using iterative as well as recursive ways. So let us discuss each approach because the time complexity of both is the same so both the solution will work absolutely fine.
A] Iterative Approach (Brute-Force method)
As we discuss that the idea is to divide the string into four parts and check if each part is valid and form its combination using 3 dots and add it to the resultant list. To check the valid part it must satisfy the below 2 conditions.
- Each part must be between 0 and 255
- No part should have leading zeros.
So we have to run a three-loop to complete the algorithm where we say that the first part is from 0 to I, the second part is I+1 to J, the third part is J+1 to K, and the fourth part is from K+1 to N(length of the string). So we can conclude the algorithm in the below steps.
- Create a function to check whether each part is valid or not.
- Create an empty list of results to store each combination
- Now we will run 3 loops.
- First will be I from 0 to n-3 which represents that it is the first part and after it, 3 parts are also there so the last 3 digits of string can never come in the first part.
- The second loop (j) will be from i+1 to n-2 which represents that the second part is after the last digit of the first past and after it, two more parts are present so the last 2 digits can never be part of the second part.
- The third loop (k) will be from j+1 to n-1 which represents that the third part is after the last digit of the second part and after it, one more part is present which should have at least one integer.
- The last part will be after k+1 to n so no loop is required for it.
👷 Now I hope that you can program this brute-force approach on your own. Below is the code snippet of implementation if you have not built the solution so take its reference and the problem will be absolutely clear to you.
def checkPart(part):
#If it is empty, space, or greater then 3 then Invalid
if len(part) < 0 or len(part) > 3:
return False
#if first char is 0 then it should only be 0
if part[0] == "0":
if len(part) != 1:
return False
#range between 0-255
if int(part) < 0 or int(part) > 255:
return False
return True
def isValidIP(s, i, j, k):
#let's form all four parts
first = s[:i+1]
second = s[i+1:j+1]
third = s[j+1:k+1]
fourth = s[k+1:]
#check if all four are valid then IP is valid
if(checkPart(first) and checkPart(second) and checkPart(third) and checkPart(fourth)):
return True
return False
def main(s):
res = [] #to store all possible combs
n = len(s)
for i in range(0, n-3):
for j in range(i+1, n-2):
for k in range(j+1, n-1):
if isValidIP(s, i, j, k):
ip = s[:i+1] + "." + s[i+1:j+1] + "." + s[j+1:k+1] + "." + s[k+1:]
res.append(ip)
return res
s = input()
res = main(s)
res.sort()
print(res)
B] Backtracking Approach
Now I hope that problem, and its solution are clear to you so let us discuss how we can solve it using backtracking. The key idea of observation here is we can select either 1 or 2 or 3 digits at a time so In each step, we will select 1, 2, 3 digits and move to next segment. Before moving we will also check that the current segment is valid of not. If it is not valid then there is no need to explore this path. Let us define the steps of Backtracking approach.
- Create check functions that accept strings and check their validity for valid IP addresses.
- We define an empty list to store all possible combinations.
- We implement a function let's say backtracking which accepts 5 arguments as an original string(s), answer, current index(denoting current index), segments used to store segments, segment index which is used to store the current number of segments we are currently in.
- The initial current index and segment index will be 0.
😆Now you must be thinking of what is the base case and when we will get the answer.
Base Case
- If the current index is equal to N and the segment index is 4 then add the current path to answer and return.
- The recursion will also break when the current index equals N and the segment index is greater than 4.
Define Constraints ~ Else we will run look three times.
- Add s[curreIndex+steps] to segment[segmentIndex]
- If the current index is valid then we will recur for the next segment and increase the current index and segment index by 1.
- Else if it is not valid then we will move to the next iteration.
👉 Let's implement the approach in Python.
#check for part is valid or not
def isValidIP(part):
if part == "" or len(part) > 3:
return False
if part[0] == "0" and len(part) != 1:
return False
if int(part) < 0 or int(part) > 255:
return False
return True
def validIPAddress(ip, answer, curridx, segment, segnum):
if curridx == len(ip) and segnum == 4:
temp = ".".join(segment)
answer.append(temp)
return
if curridx >= len(s) or segnum >= 4:
return
curr_part = ""
for i in range(1, 4):
curr_part = s[curridx: curridx+i]
if isValidIP(curr_part):
segment[segnum] = curr_part
validIPAddress(ip, answer, curridx+i, segment, segnum+1)
return
s = "23579"
global answer
answer = []
segment = [""] * 4
validIPAddress(s, answer, 0, segment, 0)
print(answer)
End Notes
Congratulations! If you have followed the tutorial till the end then I am sure that the concept of Backtracking is clear to you. We have just covered only two basic and important backtracking questions in this blog but there are many more problems to come and many more for you to solve. To only keep the blog short and your learning at a high pace we will move a little bit slow but in a very powerful way. So in the next blog we will cover the N-Queens problem, sudoku solve, and many more backtracking problem which will help you to develop your own approach when you sit and try to solve questions on any competitive site.
Thanks for your time! ✌